Искусственный интеллект высокого доверия

Ускорение вычислений и экономия памяти при тестировании больших сетей искусственных нейронов на малых выборках

Малые сети искусственных нейронов дают решения относительно низкого качества, тестировать их несложно. Проблема тестирования возникает для больших сетей искусственных нейронов, связывающих уникальный биометрический образ человека с его личным криптографическим ключом.

Тестирование качества работы большой сети искусственных нейронов по своей сложности приближается к задаче подбора криптографического ключа. Кажется, что тестирование становится невозможным, так как требует формирования огромных баз тестовых образов. Стандарт ГОСТ Р 52633.3 дает условия, при которых малых тестовых выборок оказывается вполне достаточно. Появилась возможность тестирования больших нейронных сетей на малых выборках. При таком тестировании возникают эффекты ускорения вычислений и экономии памяти по сравнению с классикой.

Зачем нужна биометрия обычному человеку

В цифровом обществе мобильность и безопасность личности во многом зависят от длины пароля доступа, которым пользуется человек^{1, 2}. Запомнить длинный пароль из случайных знаков обычный человек не может. По этой причине практически все пользуются короткими паролями доступа (левая верхняя часть рис. 1).

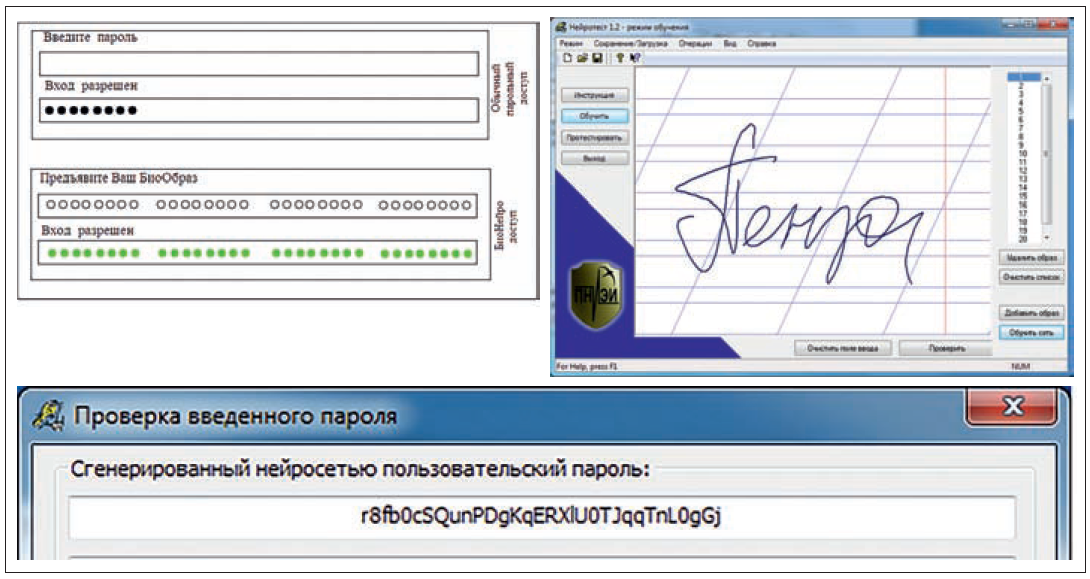Рис. 1. Две формы организации парольного доступа: короткий пароль и длинный биопароль из 32 случайных символов

Все стандартные средства ввода коротких паролей построены на сокрытии длины вводимого пользователем пароля. До процедуры парольной аутентификации нельзя сообщать сторонним лицам информацию о длине пароля. Пользователь помнит свой короткий пароль и, введя его, инициирует процедуру его хеширования. Сам пароль в операционной системе не хранится, хранится его хеш-функция.

Положение меняется коренным образом, когда речь идет о биометрикоарольной аутентификации. В этом случае от пользователя не требуется запоминания длинного случайного пароля доступа. Ему достаточно предъявить свой биометрический образ, например в виде легко запоминаемого короткого рукописного пароля "Пенза" (правая верхняя часть рис. 1). Предъявленный пример биометрического образа "свой" преобразуется обученной сетью искусственных нейронов в длинный код из 32 случайных символов пароля доступа (нижняя часть рис. 1). Запомнить такой сложный пароль обычному человеку крайне трудно. Обучение сети искусственных нейронов выполняется автоматически алгоритмом ГОСТ Р 52633.5–2011³.

При биометрико-парольной аутентификации нет смысла скрывать длину пароля в 32 случайных символа от сторонних лиц. Это максимальная длина пароля, допустимая операционной системой Windows. Хакеры, увидев длину пароля в 32 символа, который им потребуется подбирать, скорее всего, откажутся от атаки.

Упрощение задачи через переход в пространство расстояний Хэмминга

Если мы попытаемся решать задачу тестирования так, как всех нас учили в прошлом веке, то наткнемся на необходимость нарушать законодательство, собирая базы биометрических образов достаточно большого объема. Если это будут рисунки отпечатков пальцев, то потребуется где-то их взять. Лица можно скачать из социальных сетей, рисунков отпечатков пальцев в социальных сетях нет. Большие базы рисунков отпечатков пальцев недоступны.

Проще всего решить проблему, сняв свои отпечатки пальцев (девять штук, если на одном пальце обучен нейросетевой преобразователь "биометрия – код"). Можно дополнительно снять по 10 отпечатков пальца у жены и тещи. Итого мы получим тестовую выборку из 29 относительно легально полученных биометрических тестовых образов. С очень высокой вероятностью ни один из 29 тестовых отпечатков не совпадет с отпечатком "свой" и не даст ключ биометрико-криптографической аутентификации, совпадающий по всем 256 битам доступа.

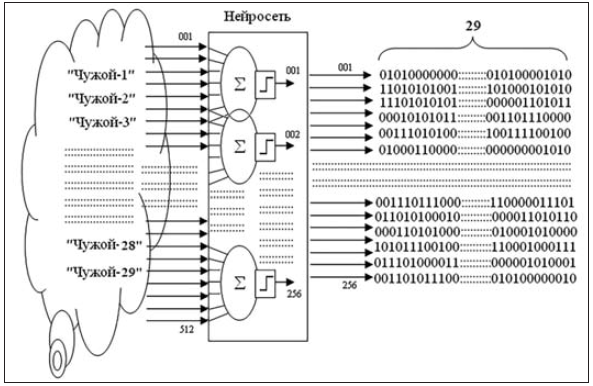
Рис. 2. Эффект "дрожания" выходных разрядов нейросети при предъявлении 29 случайных тестовых образов

Если мы подадим 29 случайных биометрических образов, то получим 29 случайных кодовых последовательностей по 256 бит, как это показано на рис. 2. Если наблюдать какой-либо выходной разряд нейросети, мы увидим почти "белый шум" не коррелированных между собой соседних бит. Если же мы попытаемся наблюдать сразу два случайно выбранных разряда нейросети, то увидим, что они уже не являются независимыми. Усредненный модуль корреляции пар выходных разрядов составит:

,

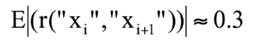что существенно больше нулевых корреляционных связей, характерных для "белого шума".

Если пытаться анализировать выходные коды длинной в 256 бит и сравнивать их между собой, мы наткнемся на высокую сложность обработки данных. В связи с этим ГОСТ Р 52633.3–2011⁴ рекомендует перейти в пространство расстояний Хэмминга между анализируемыми кодами и кодом доступа "свой":

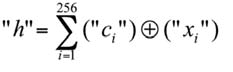(1),

где "ci" – значение i-го разряда кода "cвой"; "xi" – значение i-го разряда кода "чужой";  ⊕ – операция сложения по модулю два.

В формуле (1) и далее по тексту запись переменной в кавычках обозначает, что эта переменная целая (текстовая). Так принято во всех языках программирования, а вот в квантовой математике, чтобы различить в одном уравнении дискретные и непрерывные переменные, обычно используют скобки Дирака. Я пишу этот текст прежде всего для тех, кто умеет программировать. Применять скобки Дирака в этом тексте излишне.

Преобразование Хэмминга кардинально меняет вычислительную сложность решаемой задачи. Исходная задача анализа кодов нейросети имеет экспоненциальною вычислительную сложность, так как нам приходится анализировать статистики огромного дискретного поля в 2256 состояний. Преобразование Хэмминга (1) упрощает задачу, сводя ее к анализу дискретного поля, имеющего всего 257 состояний.

Очевидным является то, что спектр Хэмминга дискретен (существуют только целые значения положения спектральных линий («h»)). Примеры распределения положений спектральных линий Хэмминга приведены на рис. 3, из которого видно, что распределение спектральных линий Хэмминга близко к нормальному. Это следствие основной теоремы статистики. Суммирование множества случайных величин всегда приводит к нормализации. При вычислении расстояний Хэмминга (1) мы выполняем 256 суммирований по модулю "два случайных состояний" разрядов кодов, что и приводит к эффекту нормализации данных.

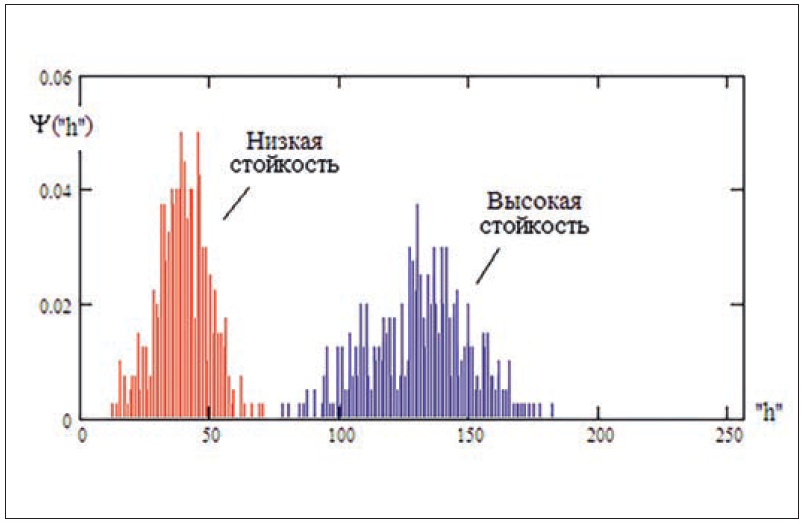
Рис. 3. Два спектра Хэмминга, принадлежащих двум разным сетям искусственных нейронов

Пользуясь этим обстоятельством, мы можем по выборке в 29 опытов вычислить:

• математическое ожидание расстояний Хэмминга – E("h");
• стандартное отклонение расстояний Хэмминга – ("h").

Далее в рамках гипотезы нормального распределения данных мы имеем возможность оценить вероятность появления ошибок второго рода:

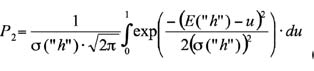(2)

Формально интеграл (2) оценивает вероятность того, когда один из случайных примеров образов "чужой" даст полное совпадение всех 256 разрядов кода с кодом образа "свой".

Рис. 3 показывает, что реальные данные тестирования могут давать значительный разброс по оценке стойкости нейросетевой биометрической защиты доступа. Так, в левой части рисунка отображены данные тестирования нейросетевой защиты, построенной на использовании относительно "слабого" биометрического образа, обладающего высокой стабильностью, но низкой уникальностью. В итоге атакующий такую биометрико-нейросетевую защиту сможет ее преодолеть с вероятностью P2 ≈ 0,001 {E("h") ≈ 40 бит и σ("h") ≈ 13 бит}.

Совершенно иная ситуация возникает, если биометрико-нейросетевая защита опирается на использование биометрического образа, обладающего приемлемой стабильностью воспроизведения и высокой уникальностью. Распределение расстояний Хэмминга в центре рис. 3 дает снижение вероятности ошибок второго рода примерно в 10 000 раз.

Ускорение вычислений и сокращение памяти вычислителя

В первом случае использования биометрического образа с относительно низкой стойкостью к атакам подбора хакеру для преодоления защиты потребуется применить примерно 10/P2 ≈ 10 000 случайных образов "чужой". Нам же для тестирования потребовалось в 330 раз меньше образов (меньше памяти компьютера) и во столько же раз меньше нам пришлось выполнять вычислений.

В ситуации применения более стойкого биометрического образа мы увеличиваем выигрыш по затратам памяти до 3 300 000 раз. Выигрыш по времени вычислений оказывается еще выше примерно в 1000 раз. Происходит это из-за того, что большая база биометрических образов уже не может разместиться в оперативной памяти обычной вычислительной машины.

Большую базу биометрических образов "чужой" приходится размещать в медленной долговременной памяти вычислительной машины и постепенно подкачивать ее из медленной долговременной памяти в быструю оперативную память. Получается, что переход в нейродинамику и наблюдение "дрожания" выходных разрядов тестируемой сети искусственных нейронов в пространстве расстояний Хэмминга является весьма и весьма эффективным приемом экономии памяти и ускорения вычислений.

Видимо, именно по этой причине наши естественные нейроны наших естественных мозгов постоянно находятся в режиме возбуждения (в режиме постоянной поддержки нейродинамики). Наблюдая шумоподобные сигналы электроэнцефалограмм^{5, 6, 7} в наших головах, скорее всего, мы наблюдаем работу нейродинамических ускорителей наших умственных способностей. Естественно, что рекомендации ГОСТ Р 52633.3–2011⁴ по ускорению тестирования сетей искусственных нейронов должны быть много примитивнее реальных процессов, происходящих в наших головах. Тем не менее существующая аналогия эффектов экономии памяти и ускорения вычислений у этих двух процессов достаточно очевидна.

Более того, оказалось, что, кроме увеличения быстродействия, искусственные нейроны, находящиеся в режиме воспроизведения нейродинамики, могут быть использованы для существенного увеличения достоверности классического статистического анализа малых выборок^{8, 9}. Все это делает исследование режимов нейродинамики одним из перспективных направлений развития науки и техники в XXI веке. В частности, подобные нейродинамические вычислители, видимо, смогут найти применение в вычислительной технике как некоторый промежуточный вариант, располагающийся между обычными компьютерами и перспективными квантовыми вычислителями. Воспроизводить программно режим нейродинамических вычислений несложно. Эта задача оказалась много проще в сравнении с попытками решать уравнения Шредингера на обычном компьютере без использования специально создаваемой квантовой логики.

¹ Иванов А.И., Чернов П.А. Протоколы биометрико-криптографического рукопожатия. Защита распределенного искусственного интеллекта интернет-вещей нейросетевыми методами // Системы безопасности. 2018. № 6. С. 54–59.
² Иванов А.И. Доверенный искусственный интеллект в защищенном исполнении для биометрии и иных важных приложений. Проблемы шифрования // Системы безопасности. 2020. №4. С. 38–39.
³ ГОСТ Р 52633.5–2011 "Защита информации. Техника защиты информации. Автоматическое обучение нейросетевых преобразователей биометрия-код доступа".
⁴ ГОСТ Р 52633.3–2011 "Защита информации. Техника защиты информации. Тестирование стойкости средств высоконадежной биометрической защиты к атакам подбора".
⁵ Боршевников А.Е., Добржинский Ю.В. О корректности модели системы высоконадежной биометрической аутентификации с использованием электроэнцефалограммы на основе стандартов ГОСТ Р 52633 // Сборник научных статей по материалам II Всероссийской научно-технической конференции "Безопасность информационных технологий", 24 июня. Пенза, 2020. С. 70–74.
⁶ Гончаров С.М., Боршевников А.Е. Михайлов А.Г., Апальков А.Ю. Восстановление секретного ключа на основе электроэнцефалограмм при движении глаз с закрытыми веками // Информация и безопасность. Т. 19. № 1. 2016. С. 114–117. (Свободный доступ через национальную электронную библиотеку eLIBRARY).
⁷ Гончаров С.М., Боршевников А.Е. Прогнозирование выходных параметров нейросетевого преобразователя "биометрия – код доступа" на основе электроэнцефалограммы // Информация и безопасность. Т. 21. № 3. 2018. С. 302–307. (Свободный доступ через национальную электронную библиотеку eLIBRARY).
⁸ Иванов А.И., Банных А.Г., Безяев А.В. Искусственные молекулы, собранные из искусственных нейронов, воспроизводящих работу классических статистических критериев // Вестник пермского университета. Серия: Математика. Механика. Информатика. 2020. № 1 (48). С. 26–32. (Свободный доступ через национальную электронную библиотеку eLIBRARY).
⁹ Иванов А.И. Искусственные математические молекулы: повышение точности статистических оценок на малых выборках (программы на языке MathCAD): препринт. Пенза: из-во Пензенского государственного университета", 2020. 36 с. ISBN 978-5-907262-42-3 (свободный доступ через национальную электронную библиотеку eLIBRARY).

Опубликовано в журнале "Системы безопасности" №5/2020

Иллюстрации предоставлены автором

Фото: ru.freepik.com