Микропотребление нейроморфных вычислителей: почему это возможно и технически целесообразно?

Маккалок и Питтс в своей классической работе 1943 г. предложили убедительную парадигму вычислений в нейробинарной логике. Тогда не было электронных вычислительных машин и модемов для их взаимодействия, поэтому нейробинарную логику Маккалока – Питса необходимо подгонять под сегодняшние реалии и вводить модем, передающий внутри нашего мозга импульсы по очень "плохой" длинной линии аксонов естественных нейронов. Простое копирование природы с заменой таких модемов USB-протоколами уже дает огромное снижение энергопотребления искусственными нейроморфными вычислителями, но причин многократного снижения энергопотребления никто не объясняет.

С высокой вероятностью эффект снижения потребления энергии при одновременном росте эффективного быстродействия возникает из-за "туннельных" переходов барьера между непрерывными (континуальными) и дискретными (логическими) вычислениями.

Чем больше таких барьеров содержит архитектура нейроморфного вычислителя, тем больше эффект экономии энергопотребления или, что почти то же самое, ускорения направленных переборов.

Маркетинговые уловки перехода от обычных процессоров к многоядерным

Начиная с работы Маккалока и Питтса 1943 г. [1] параллельно с развитием технологии нейрологических вычислений создавались обычные электронные вычислительные машины в форме ламповых ЭВМ, далее транзисторных ЭВМ, далее на микросхемах низкой степени интеграции, далее на микросхемах высокой степени интеграции.

Чем выше была степень интеграции процессоров, тем выше был уровень брака. При этом потребитель платит за все. И за годный процессор производства фирмы Intel, и за стоящую рядом с ним корзину брака. Каков процент брака, никто не знает, это коммерческая тайна. Предположим, что в брак уходило 99% процессоров, а 1% годных процессоров продавался по 200 долларов США в 1995 г. за 1 штуку.

Это означает, что каждый годный процессор должен стоить всего 2 доллара, однако из-за высокого уровня брака стоимость процессора вырастает примерно в 100 раз. Такое происходит потому, что слишком много транзисторов упаковано на каждый квадратный миллиметр площади кристалла. Кремневый кристалл нельзя вырастить идеальным. Он обязательно будет содержать дефекты. Если транзистор триггера или логического элемента точно попадет на такой дефект, то мы получим бракованный процессор.

Определить на глазок, что тот или иной процессор бракованный, нельзя. Нужно обязательно разрезать кремневую пластину на квадратики, разместить их в корпусах, а далее приварить тонкими золотыми нитями площадки кристалла к ножкам почти готового процессора. Далее почти готовый процессор уходит на логическое тестирование. Именно логический тест дает самый большой процент брака.

После медленного логического теста выполняют динамический тест на высокой тактовой частоте. Этот тест оценивает то, сколько "подпаленных" (почти исправных) транзисторов находится слишком близко к дефектам кристалла. Такие транзисторы нормально работают (почти не греются), если тактовая частота занижена. На высокой тактовой частоте "подпаленные" транзисторы греются и нагревают весь кристалл. Однако производитель может указать на корпусе процессора, рекомендуемую заниженную тактовую частоту и продать такой товар по заниженной стоимости. Это уже маркетинг, когда производитель различными уловками пытается продать какую-то часть корзины с браком.

Еще одним сильным маркетинговым ходом является дробление содержания процессора на несколько одинаковых ядер. Если объявить пользователям, что процессор имеет 16 ядер, а реально разместить на его кристалле 20 ядер, то можно снизить брак в четыре раза. Вместо корзины с 99% брака для одноядерных процессоров мы получим корзину с 75% брака для 16-ядерных процессоров. Этот маркетинговый ход вполне реален, если все дефекты кристалла попадают только на четыре "подпаленных" ядра.

В этом случае их можно обнаружить и просто отключить (сжечь перемычки, питающие "подпаленые" ядра). Если дефектными оказываются пять ядер, то их тоже можно отключить, однако пользователю придется сообщить об этом. Это почти то же самое, что и продавать процессоры с заниженной тактовой частотой.

Путь повышения числа ядер в процессорах выгоден производителю из-за ощутимого снижения корзины брака. По этой причине появились процессоры с 32, 64 и даже с 1 024 ядрами. Все это подается производителями как стремление к возможному линейному распараллеливанию вычислений. Формально на процессоре с 1 024 ядрами можно ускорить вычисления в 1 024 раза, если удастся написать программу, равномерно загрузившую все 1 024 ядра. Как этого добиться – вопрос открытый. Чем больше ядер, тем "легче" должны быть связи между ними. Наличие даже одной "тяжелой" связи между двумя ядрами может сильно затормозить вычислительный процесс в целом.

Бионика связей естественных нейронов живых существ

Следует отметить, что парадигма бинарных нейрологических вычислений впервые была сформулирована Питтсом и Маккалоком в 1943 г. [1] и послужила стартом для ряда последующих исследований. В 1949 г. Дональд Хэбб [2] опубликовал первый работоспособный алгоритм обучения искусственных нейронов. Еще один значимый шаг сделал нейрофизиолог Фрэнк Розенблатт в 1957 г., создавший в Корнуэльской лаборатории аэронавтики персептрон. Он же создал первый программный эмулятор нейрокомпьютера "Марк-1" на цифровой вычислительной машине IBM-704 в 1960 г. Это оказало огромное влияние на общественное внимание к тематике создания нейрокомпьютеров.

Гораздо более быстрыми темпами в 40-х и 50-х гг. прошлого века развивались обычные на сегодня бинарные компьютеры с обычной булевой логикой. К настоящему времени вычислительных ресурсов бинарной логики вполне достаточно, однако их возможности значительно уступают возможностям естественных вычислителей людей и иных живых существ. Так, мы, люди, способны в реальном времени решать 10 000-мерные задачи. У нас и у животных присутствуют большие пирамидальные естественные нейроны с 10 тыс. входами (это не гипотеза, а патологоанатомический факт).

Во многом теория искусственных нейронов строилась дублированием логики развития бинарных компьютеров. Это обусловлено простотой моделирования персептронов и искусственных нейронов с непрерывными выходными функциями. При моделировании на обычных компьютерах не возникает проблемы обеспечения питания вычисляющих элементов, нет проблемы поддерживания состояний "0" или состояний "1" на выходах обычной булевой логики или на выходе персептрона Розенблатта.

Совершенно иная ситуация возникает в живых организмах: естественные нейроны не имеют доступа к общему источнику электропитания.
Каждый нейрон вынужден самостоятельно вырабатывать энергию на каждый выходной импульс. Передача данных между естественными нейронами живых существ выполняется пачками импульсов [3, 4], как это отражено на рис. 1.

Рис. 1. Естественный нейрон одновременно является и вычислителем, и "модемом" передачи данных по длинной линии – аксону (импульсы – это вынужденный прием, являющийся следствием отсутствия "батареек" внутри "нейромодема")

Выходной отросток естественного нейрона (аксон) имеет длину в десятки раз больше тела нейрона. Аксоны играют роль длинных "плохих" проводов передачи информации с очень плохой изоляцией. Формально естественный нейрон одновременно выполняет вычисления и параллельно – роль "модема", передающего информацию. Так как проводящие свойства аксонов много хуже проводящих свойств хорошо изолированных медных проводов, аксоны нейронов не могут быть слишком длинными.

В первом приближении импульсы в аксонах можно рассматривать как реализацию некоторых протоколов передачи информации "нейромодемов/электрогенераторов". При этом передача электроимпульсов по медным хорошо изолированным проводам может обеспечить скорость передачи, близкую к скорости света. Передача информации внутри живых существ по "плохим" проводам аксонов с плохой электроизоляцией обеспечивает передачу информации только с скоростью звука (примерно в миллион раз медленнее скорости света).

Концепция нейросетевой молекулы, преобразующей высокоразмерный входной континуум в дискретный спектр выходных состояний

Заметим, что если бы была верна бинарная гипотеза Питтса – Маккалока [1], то физиологи могли бы наблюдать только отклики бинарных естественных нейронов. В этом случае нейроны должны выдавать один импульс, соответствующий состоянию "0", либо должны выдавать два импульса, соответствующие состоянию "1".

Физиологи же наблюдают пачки импульсов [3] на аксонах естественных нейронов (на рис. 1 изображена пачка из двух импульсов и пачка из пяти импульсов). То есть, оставаясь в рамках парадигмы Питтса – Маккалока [1], мы должны констатировать то, что логика естественных нейронов является Q-арной, а не бинарной.

Переходя к замене бинарной нейрологики Q-арной нейрологикой, мы вынуждены заменить в модели естественного нейрона Питтса – Маккалока бинарный персептрон на более сложный искусственный нейрон с Q-арным выходным квантователем. На рис. 2 приведена модель естественного нейрона, состоящая из Q-арного персептрона и выходного модема для передачи данных по "плохой" длинной линии аксона.

Рис. 2. Представление естественных нейронов в виде программной нейромолекулы, воспроизводящей эффект континуально-квантового перехода на микроуровне

Заметим, что в начале XXI века значительное внимание уделяется попыткам создания квантовых вычислителей, воспроизводящих на физическом уровне эффекты квантовой суперпозиции [4]. В этом контексте конструкцию рис. 2 мы имеем право считать некоторой программной реализацией нейромолекулы, воспроизводящей, например, свойства молекулы водорода. В этом случае Q-арный выходной квантователь должен иметь число выходных состояний (число ступенек), точно совпадающее с числом спектральных линий молекулы водорода. Спектр линий водорода приведен в нижней части рис. 3.

Рис. 3. Решение волнового уравнения для атома водорода, показывающее положение континуумов вероятного появления электронов (электронных облаков) для разных значений волновых чисел

Показатель Q-арности (система счисления), в которой обучен естественный или искусственный нейрон, играет крайне важную роль [5]. В этом контексте физиолог, желающий оценить значение данного параметра, должен по экрану осциллографа [3] вести документирование числа импульсов в пачках конкретного аксона.

Разница между максимальным числом импульсов и их минимальным числом будет являться оценкой числа выходных состояний квантователя одного естественного нейрона.

Следует отметить, что молекула водорода имеет порядка 32 спектральных линий, то есть нейромодель молекулы водорода должна иметь выходной квантователь Q ≈ 32. Возможен иной вариант, когда модель собирается из нескольких искусственных нейронов [6], в этом случае сами нейроны могут быть бинарными. Если модель состоит из –n искусственных бинарных нейронов, то число выходных состояний нейросетевой молекулы составляет Q = 2ⁿ возможных выходных состояний.

Последние 30 лет физико-математическая общественность значительное внимание уделяет квантовым вычислениям и квантовой информатике [7, 8]. Формально это все можно свести к попыткам перенести вычисления на микроуровень молекулы водорода и найти условия, при которых она сможет играть роль квантового триггера или иного квантово-логического элемента. Как это все должно выглядеть со стороны математики и программирования, подробно изложено во множестве работ [7, 8].

Бумага способна отобразить любую сколь угодно сложную математическую конструкцию, однако доверие к ней возникает, если удастся ее подтвердить практикой. Параллельно с бумагой всегда должны создаваться физические реализации новых принципов вычислений. В этом контексте особенных успехов пока нет. Вполне возможно, что их не будет в обозримом будущем.

Моя убежденность в этом опирается на бионику. Видимо, природа уже давно создала условия воспроизведения эффектов квантовой суперпозиции в наших головах (рис. 1). Естественные нейроны ведут себя примерно так же, как и физические молекулы. Модем внутри естественного нейрона – это окончание абсолютно устойчивого фрагмента континуально-квантовых вычислений. При этом нет необходимости в жидком гелии, ионных ловушках, микрополяризаторах, а также синтезе нужных дефектов в кристалле алмаза.
Вполне достаточно полужидкого "холодца" в наших головах при температуре от 22 до 42 °С и погруженных в этот "холодец" наших естественных нейронов.

Сегодняшним программистам и инженерам не следует ждать, когда в Зеленограде или на Тайване испекут для них микросхемы или микропроцессоры с квантовой логикой на новых физических принципах. В этом контексте нужно брать то, что уже есть, и копировать природу.
В результате мы получим так называемые нейроморфные конструкции [9]. Оказалось, что для кардинального снижения энергопотребления при очень сложных вычислениях достаточно в аппаратно-программной среде, эмулирующей искусственные нейроны, соединять ядра, их реализующие, через USB-протоколы. Вместо нейромодемов перед аксонами по рис. 1 вполне могут быть использованы USB-протоколы для передачи данных между ядрами современных процессоров. Как все оказалось просто и непритязательно! Думаю, что это видимость простоты, под ней лежит очень серьезная математика, которая пока еще на бумаге до конца не формализована.

Некоторые полезные аналогии с уже созданной математикой квантовых вычислений

Строгая математика квантовых вычислений построена на понятии кубита [7, 8]. То, на сколько дрожание выходных бит нейросетевого преобразователя [10] близко к теоретической модели кубита, – вопрос открытый. Однако при тестировании нейросети по рекомендациям ГОСТ Р 52633.3–2011 [11] биты выходного кода нейросети начинают "дрожать", как это показано на рис. 4, и именно учет статистик этого "дрожания" позволяет ускорять вычисления и экономить память вычислителя.

Рис. 4. Эффект "дрожания" выходных разрядов нейросети при предъявлении 30 случайных тестовых образов

Из рис. 4 видно, что для каждого из 30 тестовых образов "чужой" мы наблюдаем некоторый фрагмент 256-кубитной квантовой суперпозиции. Если обработка каждого образа длится 10 мс, то мы программно поддерживаем эффект квантовой суперпозиции 300 мс. Если этого времени нам недостаточно, то мы имеем возможность программно поддерживать эффект квантовой суперпозиции во много раз дольше за счет скрещивания между собой образов "чужой" по ГОСТ Р 52633.2–2010 [12].

Из каждой пары образов-родителей "чужой-n" удается получать 1, 2, 3,.. образов потомков и тем самым существенно увеличивать время поддержки квантовой суперпозиции. Формально следует добиваться того, чтобы времени поддержки квантовой суперпозиции было достаточно для решения поставленной задачи.
Отметим, что этот подход снимает проблему как выбора достаточно большого числа кубит, так и поддержки интервала времени их квантовой суперпозиции достаточного для решения задачи. Число кубит задается числом нейронов в сети, а время поддержки задается числом, используемым при моделировании примеров тестовых образов.

Гарантией того, что при тестировании нейросетевых преобразователей мы действительно наблюдаем что-то похожее на предсказанные на бумаге кубиты, является огромное ускорение тестирования и огромное сокращение потребностей в памяти [10].

Аналог понятия квантовой запутанности (квантовой сцепленности)

Кроме базового понятия “кубит”, важным является понятие "квантовая сцепленность". Корректная теория квантовой сцепленности (квантовой запутанности) для больших размерностей пока еще не создана. По этой причине укажем только метод ее оценки на данных среды моделирования "БиоНейроАвтограф" [13].

Среда моделирования [13] предназначена для проведения лабораторных работ студентами русскоязычных университетов без нарушения закона о персональных биометрических данных. Студент задает псевдослучайным программным генератором свой личный ключ длинной в 256 бит. Запомнить его студент не может, однако он может написать своим почерком манипулятором "мышь" одну или две буквы легко запоминаемого рукописного пароля. Для обучения нейросети нужно восемь и более примеров рукописного пароля "свой". После автоматического обучения нейросети проверочный пример рукописного пароля "свой" должен точно воспроизводить заданный ключ.

Если же манипулятором "мышь" студент пишет другой рукописный пароль, то на выходе преобразователя "биометрия – код" появляется случайный код. При этом для каждой реализации одного и того же рукописного пароля одним почерком будут появляться разные коды. Примеры двух таких кодов приведены на рис. 5.

Рис. 5. Пример двух откликов нейросетевого преобразователя биометрии в код длиной 256 бит на двух разных примерах одного рукописного пароля "чужой"

Беглое сравнение двух длинных ключей позволяет убедится в том, что они разные (случайные), однако должны иметь между собой и существенное сходство. Их писал один и тот же человек, воспроизводя один и тот же рукописный пароль. Оценить уровень сходства удается, если вычислить коэффициент корреляции между двумя бинарными последовательностями одинаковой длины.

При оценке коэффициента корреляции используется классическая формула конца XIX века:

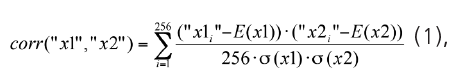
где Е(.) – операция вычисления математического ожидания; σ(.) – операция вычисления стандартного отклонения.

Если данные независимы, то функционал (1) должен давать малые по модулю значения. Если данные зависимы, то ситуация меняется.

Для среды моделирования "БиоНейроАвтограф" коэффициент корреляционной сцепленности будет составлять примерно 0,33 для одинаковых рукописных паролей, написанных почерком одного и того же студента. Это и есть оценка показателя квантовой запутанности (сцепленности) между состояниями 256-кубитной квантовой суперпозиции.

Эффект огромной экономии памяти при хранении информации во время тестирования

Проще всего убедиться в огромной экономии памяти при применении нейроморфных вычислительных структур, опираясь на международный стандарт ИСО/МЭК 19795–1–2007 [14] и на национальный стандарт России ГОСТ Р 52633.3–2011 [11]. Интервал между введением в действие этих двух документов всего четыре года, но они отражают взгляды двух совершенно разных эпох. Международный стандарт отражает "гладкие" знания о работе с континуумами, а стандарт России уже опирается на "нейроморфные" архитектуры вычислений.

Так, если мы имеем вероятность ошибок второго рода P₂ ≈ 0,0000000001 (такая вероятность вполне реальна для рукописных паролей среды моделирования "БиоНейроАвтограф" [13]), то по рекомендациям международного стандарта нам нужна тестовая база рукописных паролей "чужой” объемом в 30 млрд примеров. Технически сформировать базу биометрических образов столь значительного объема крайне сложно, кроме того, законодательства практически всех стран накладывают значительные ограничения на сбор, хранение и использование баз реальных биометрических образов большого объема.

Если такая база будет создана каким-то из университетов, то ее использование для проведения работ студентами наткнется на жесткие законодательные ограничения. Даже простое хранение такой базы потребует привлечения нескольких серверов университета, имеющих примерно 1 000 Гбайт памяти. Хранить даже обезличенную биометрию реальных пользователей в облаках без ее шифрования нельзя.

Ситуация коренным образом меняется, если мы опираемся на национальный стандарт России [11]. Этот стандарт не требует сбора огромной тестовой базы биометрических образов. По его рекомендациям достаточно 30 образов "чужой", каждый должен быть представлен 20 примерами. Далее стандарт рекомендует перейти от анализа обычных кодов длинной в 256 бит к их расстояниям Хэмминга по отношению к коду "свой":

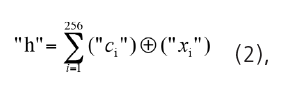
где "с_i" – i-й разряд известного при обучении кода "свой"; "х_i" – i-й разряд отклика на образ "чужой"; ⊕ – операция сложения двух разрядов по модулю два.

Принципиально важным является то, что свертка данных (2) экспоненциально снижает размерность задачи с 256-мерной до одномерной. Кроме того, свертка данных (2) является хорошим нормализатором распределения ее выходных состояний. То есть из пространства обработки дискретных данных (2) мы можем вернуться к континуальным представлениям, через вычисление математического ожидания E("h") и стандартного отклонения σ("h") расстояний Хэмминга.

Математическое ожидание E("h") и стандартное отклонение σ("h") уже являются континуумами. Опираясь на них и на гипотезу нормального распределения, мы можем предсказать вероятность ошибок второго рода, минуя сбор, хранение, использование огромной базы биометрических тестовых образов. Возникает экономия памяти примерно в миллиард раз. Нет необходимости привлечения облаков и серверов, вполне достаточно офисной вычислительной машины для выполнения лабораторной работы студентом любого русскоязычного университета.

Заметим, что все вышесказанное относится к нейроморфным вычислениям, ориентированным на обработку биометрических данных студентами со скромными вычислительными ресурсами. При этом оптимизм по поводу нейроморфных вычислений значительно усиливается в силу того, что многократный переход континуально-квантового барьера приводит к накоплению выигрыша по экономии памяти [10] и по экономии энергопотребления.

Почти физическое гиперраспараллеливание вычислений в нейроморфных архитектурах

В начале статьи было показано, что увеличение числа ядер в современных процессорах является предпосылкой для линейного распараллеливания вычислений: чем больше ядер, тем больший потенциал распараллеливания у того или иного процессора. Однако как воспользоваться этим потенциалом, неизвестно.

Очевидно, что создать программу, "хорошо" распараллеливающую вычисления между небольшим числом ядер, проще, чем программу, "хорошо" распараллеливающую вычисления между большим числом ядер. В этом контексте нейросетевые преобразования выгодно отличаются от обычных вычислений, если обмен данными между нейронами минимален и нейроны заранее предобучены на все случаи жизни. Такая ситуация не возникает сама по себе, ее нужно изначально создавать. Например, такая ситуация возникает для сетей, обучающихся "на лету" [15], нейроны которых воспроизводят работу классических статистических критериев. В этом случае каждое ядро процессора может содержать существенно разное программное обеспечение, но все они не нуждаются в программировании (все они заранее предобучены, заранее запрограммированы).

В заранее запрограммированные ядра нужно только подавать реальные данные, а они будут откликаться состоянием "0" или "1" их бинарных нейронов. Кажется, что это та же самая схема линейного распараллеливания вычислительной нагрузки между ядрами-нейронами. На самом деле это далеко не так.

Оказалось, что внесение минимальных изменений в программу каждого из ядер (группу нейронов одного ядра) позволяет существенно снизить потребность в числе необходимых ядер процессора [16, 17]. Так, если заменить бинарные нейроны Q = 2 на троичные нейроны Q = 3 (в программе квантователей нейрона добавляется еще одно условие сравнения), необходимое число ядер процессора значительно снижается. В работе [16] столь примитивное изменение позволяет вместо 300 бинарных искусственных нейронов использовать 30 троичных нейронов. Число ядер процессора сократилось в 10 раз при одной и той же достоверности принятия решения.

В итоге мы получаем 10-кратное снижение энергозатрат при том же уровне достоверности принимаемых решений. Кроме того, практика программирования показала, что дальнейшее увеличение Q-арности нейронов, воспроизводимых каждым ядром процессора, приводит к дальнейшему росту эффективности вычислений (снижению энергозатрат). Расплачиваться за это приходится только усложнением предобучения искусственных нейронов. Усложняется не техническая реализация вычислителя, а предобучение (предварительное программирование каждого конкретного ядра).

На данный момент предсказать влияние роста Q-арности нейронов на снижение потребления и усложнение обучения не удается. Сегодня это можно сделать только опытном путем через затраты на реальное программирование и на реальное тестирование.

Перечисленные выше возможности принципиальны для повышения безопасности нейросетевой биометрии. Современные многоядерные процессоры – это не более чем удобная абстракция. В реальном мире необходимо нейросетевую биометрию уплотнить до размещения в доверенном контроллере СИМ-карты или RFID-карты. Такой шаг позволит существенно повысить уровень информационной безопасности поддержки цифровых гражданских прав личности. Хотелось бы, чтобы этот важный шаг поддержки цифровых гражданских прав первой сделала Россия.

Литература:

1. McCulloch, Warren S.; Pitts, Walter (1943). "A logical calculus of the ideas immanent in nervous activity". Bulletin of Mathematical Biophysics. 5 (4): 115–133.
2. Donald Olding Hebb. The Organization of Behavior: A Neuropsychological Theory. Wiley, 1949.
3. Николлс Д., Мартин Р., Валлас Б., Фукс П. От нейрона к мозгу. Пер. с англ. П. Балабана, А. Галкина, Р. Гиниатуллина, Р. Хазипова, Л. Хируга. М.: Едиториал УРСС, 2003. 672 с.
4. Волчихин В., Иванов А., Фунтиков В., Малыгина Е. Перспективы использования искусственных нейронных сетей с многоуровневыми квантователями в технологии биометрико-нейросетевой аутентификации // Известия высших учебных заведений. Поволжский регион. Технические науки. 2013. № 4. С. 88–99.
5. Малыгина, Е. Биометрико-нейросетевая аутентификация: перспективы применения сетей квадратичных нейронов с многоуровневым квантованием биометрических данных: препринт. Пенза: Изд-во ПГУ. 2020. 114 с.
6. Иванов А. Искусственные математические молекулы: повышение точности статистических оценок на малых выборках (программы на языке MathCAD): препринт. Пенза: Изд-во Пензенского госуниверситета. 2020. 36 с.
7. Нильсон М., Чанг И. Квантовые вычисления и квантовая информация. М.: Мир. 2006 г. 821 с.
8. Душкин Р. Квантовые вычисления и функциональное программирование. ДМК Пресс. 2015. 234 с.
9. Сандомирская Ю. Искусственный интеллект и нейроморфные вычисления: второе дыхание // Коммерсантъ наука. 2021. № 47. С. 26–29.
10. Иванов А. Искусственный интеллект высокого доверия: ускорение вычислений и экономия памяти при тестировании больших сетей искусственных нейронов на малых выборках // Системы безопасности. 2020. № 5. С .60–62.
11. ГОСТ Р 52633.3–2011 Защита информации. Техника защиты информации. Тестирование стойкости средств высоконадежной биометрической защиты к атакам подбора.
12. ГОСТ Р 52633.2–2010 Защита информации. Техника защиты информации. Требования к формированию синтетических биометрических образов, предназначенных для тестирования средств высоконадежной биометрической аутентификации.
13. Иванов А., Захаров О. Среда моделирования "БиоНейроАвтограф". Программный продукт, создан лабораторией биометрических и нейросетевых технологий, размещен с 2009 г. на сайте АО "ПНИЭИ" http://пниэи.рф/activity/science/noc/bioneuroautograph.zip для свободного использования любым русскоязычным университетом.
14. ГОСТ Р ИСО/МЭК 19795–1–2007 Автоматическая идентификация. Идентификация биометрическая. Эксплуатационные испытания и протоколы испытаний в биометрии. Часть 1. Принципы и структура.
15. Иванов А. Бионика: обучение "на лету" с использованием генетически по-разному предобученных искусственных нейронов // Системы безопасности. 2023. № 4. С. 122–125.
16. Волчихин В., Иванов А., Иванов А., Ерёменко Р., Савинов К. Номограммы для сравнения корректирующих способностей бинарных и троичных нейронов, используемых при многокритериальной проверке гипотезы независимости данных малых выборок. //Известия вузов. Поволжский регион. Технические науки. 2022. № 4. С. 5–16.
17. Иванов А., Савин К., Еременко Р. Эффект перехода от применения бинарных искусственных нейронов к троичным нейронам при совместном использовании пяти классических статистических критериев проверки гипотез нормальности или равномерности распределений малых выборок // Вестник Пермского университета. Математика. Механика. Информатика. 2022. Вып. 3 (58). С. 59–67.

Опубликовано в журнале "Системы безопасности" № 6/2023

Все статьи журнала "Системы безопасности"
доступны для скачивания в iMag >>

Фото: ru.freepik.com